Das CRR-Modell - Teil 1: Grundlagen

Einführung

Ein besonders einfaches und gut zugängliches Finanzmarktmodell ist das Cox-Ross-Rubinstein-Modell (kurz CRR-Modell). Das hat u.a. die folgenden Gründe:

• Es handelt sich in der Tat um ein sehr simples Modell. Es genügen wenige mathematische Grundlagen, um es verstehen- und anwenden zu können.
• Das CRR-Modell ist ein möglicher Ausgangspunkt, um das prominentere Black-Scholes-Modell herzuleiten.
• Das Modell lässt sich sehr einfach implementieren (beispielsweise mit Python, aber auch mit Excel).

rotz (oder gerade wegen) seiner Einfachheit, wird das CRR-Modell immer noch angewendet. Üblicherweise wird dieses Modell für das Pricing & Hedging von Derivaten benutzt. In der Kapitalmarkttheorie wird am Anfang gerne das CRR-Modell herangezogen. Variiert man das Modell etwas, kann man damit auch Kreditausfälle modellieren. Banken können dann einem Kredit einen "fairen" Wert zuordnen. Das ist wichtig, um die Konditionen für einen Kredit sinnvoll festzulegen (also der Zins, den der Kunde Zahlen muss und ggf. weitere Spesen).

Man bedenke, dass dieses Modell immerhin bereits seit dem Ende der 1970er bekannt war. Es wurde 1979 in der Arbeit Option pricing: a simplified approach von den Namensgebern Cox, Ross und Rubinstein eingeführt. Man kann aber davon ausgehen, dass viele der hier vorgestellten Vorgehensweisen wahrscheinlich schon deutlich früher Verwendung fanden.

In der folgenden Einführung wird weitgehend versucht auf (für Anfänger möglicherweise hinderliche) Details zur Modellierung zu verzichten. Der Kenner möge mir dies verzeihen, und ich will an dieser Stelle darauf hinweisen, dass ein solides Fundament an Maß- und Wahrscheinlichkeitstheorie notwendig ist, wenn man finanzmathematische Theorien bis ins letzte Detail verstehen will. Insofern richten sich die folgenden Zeilen an Anfänger und Praktiker. Dennoch wird ein solides mathematisches Grundwissen vorausgesetzt (insb. zur Wahrscheinlichkeitstheorie).

Grundlagen des CRR-Modells

Man stelle sich zunächst einen Investor vor, der nur zwei Wertpapiere handelt. Ein "risikoloses" (Bond) und ein "risikobehaftetes" Asset (Aktie). Das risikolose Asset stelle man sich am besten wie ein Tagesgeldkonto oder Girokonto vor (insb. im Fall der meisten Privatinvestoren mit einem Nettovermögen von weniger als 100 TEUR). Das am wenigsten risikoreiche Asset ist eine Anleihe bester Bonität, mit kurzer Laufzeit (weniger als zwei Jahre). Das risikobehaftete Asset könnte grundsätzlich jedes andere Wertpapier sein. Hier nur eine kleine Auswahl: Aktien, Staatanleihen mit einer Bonität schlechter als BBB und/oder längerer Laufzeit (zehn Jahre oder mehr), Unternehmensanleihen, die meisten Derivate, ETFs, etc.

Im folgendem nehmen wir weiterhin an, dass wir einen unregulierten Finanzmarkt haben. Es gibt also keine Handelsbeschränkungen. Der Investor kann einen beliebig hohen Kredit aufnehmen (zur Frage wie sich das im Modell äußert später mehr) ,und beliebig granulare Anteile der beiden Wertpapiere kaufen und verkaufen (d.h., dass der Investor beispielsweise auch 0.004 Anteile einer Aktie kaufen könnte). Abgesehen davon, nehmen wir an, dass der Investor keine Gebühren oder Steuern zahlen muss. Zu guter Letzt nehmen wir an, dass keine Dividenden ausgezahlt werden.

Der Investor startet zu einem gewissen Zeitpunkt \( t_0 \) mit dem Handel. Der Handel endet zu einem Zeitpunkt \( t_N \) mit \( N \in \mathbb{N} \). Das CRR-Modell ist ein diskretes Modell, d.h. hier, dass nur an endlich vielen Zeitpunkten \( t_0, t_1 \cdots, t_n \) gehandelt wird. Im folgendem sei zur Vereinfachung immer \( t_n = n \). \( t_n \) kann man sich als Jahr, Monat, Woche, Tag oder Minute vorstellen. Üblicherweise nimmt man an, dass die Zeitabschnitte äquidistant sind.

Wir kommen nun zum Bond. Der Preis des Bonds zum Zeitpunkt \( n \) wird mit \( S^0_n \) bezeichnet. Dabei ist \( S^0_n = (1 + r)^n \) mit einen risikolosen Zins \( r > -1 \). Wir nehmen dabei an, dass der Zins über dem gesamten Zeitraum konstant bleibt.

Den Preis einer Aktie zum Zeitpunkt \( n \) bezeichnen wir als \( S^1_n \), wobei der Startpreis \( S^1_0 > 0 \) von Anfang an bekannt ist. Hier kommen wir zu einer weiteren wesentlichen Annahme des Modells. Wir gehen davon aus, dass der Preis der Aktie nach jeder Zeiteinheit um einen festen Prozentsatz sinkt (down) oder steigt (up). Weitere Preisänderungen werden ausgeschlossen. Damit gilt für den Preis der Aktie \( S^1_n = S^1_0 \cdot \prod_{j=1}^n (1 + R_j) \) mit \( R_j \in \{ r_{d}, r_{u} \} \). Wir bezeichnen dabei die Wahrscheinlichkeiten mit \( p_d := \mathbb{P}[R_j = r_d] > 0 \) und \( p_u := \mathbb{P}[R_j = r_u] \) (mit \( p_u = 1 - p_d \)). D.h., dass die Wahrscheinlichkeit für die eine oder andere Preisentwicklung nach jeder Zeiteinheit identisch ist. Wir nehmen damit implizit an, dass \( (R_j)_{j = 1, \cdots, n} \) unabhängige Zufallsvariablen sind.

Um später dem Umstand Rechnung zu tragen, dass sich das Risiko beim Kauf der Aktie lohnen sollte (man verzichtet dafür schließlich auf die sichere Rendite des Bonds), führen wir noch die diskontierten Preisprozesse ein, also \( X^1_n := \frac{S^1_n}{(1+r)^n} \) (man beachte, dass für den Bond immer \( X^0_n := \frac{S^0_n}{(1+r)^n} = 1 \) gilt).

Die Menge aller Aktien, die gekauft oder verkauft werden, wird mit \( \xi^1_n \in \mathbb{R} \) bezeichnet. Ist \( \xi^1_n \) positiv, so kauft der Investor die entsprechende Menge an Aktien. Ist der Wert negativ, so werden die Aktien verkauft (Leerverkauf). Einen Leerverkauf kann man sich wie ein Kreditgeschäft vorstellen. Der Investor leiht sich die Aktien und verkauft diese dann. Nach einer gewissen Zeit kauft er sie zurück (um die Aktien zurückzugeben). Ist der Preis der Aktie in dieser Zeit gesunken, hat der Investor einen Gewinn gemacht. Die Menge, die der Investor in den Bond investiert, wird analog mit \( \xi^0_n \in \mathbb{R} \) bezeichnet. Ist dieser Wert positiv, kann man das so interpretieren, dass der Investor Fremdkapital verleiht, und dafür den entsprechenden risikolosen Zins bekommt (z.B. durch ein Tagesgeldkonto). Andernfalls nimmt der Investor zum Zinssatz \( r \) Schulden auf. Ich will an dieser Stelle noch darauf hinweisen, dass die Werte für \( \xi^0_n \) und \( \xi^1_n \) bereits zum Zeitpunkt \( n-1 \) bekannt sind (anders als der Aktienpreis). Technisch sagt man, dass entsprechende Zufallsvariablen "vorhersehbar" sind (im Fall der Aktienpreises spricht man von Adaptivität). Diese Eigenschaft wird sich als nützlich erweisen, wenn man mit bedingten Erwartungswerten rechnet.

Man beachte, dass der Wert des Gesamtportfolios den Wert

\[ V_n := \xi^0_n \cdot S^0_n + \xi^1_n S^1_n \]

\[ = \xi^0_n \cdot (1 + r)^n + \xi^0_n \cdot S^1_0 \cdot \prod_{j=1}^n (1 + R_j) \]

hat. Wir nennen \( (V_n)_{n = 1, \cdots, N} \) Wertprozess.

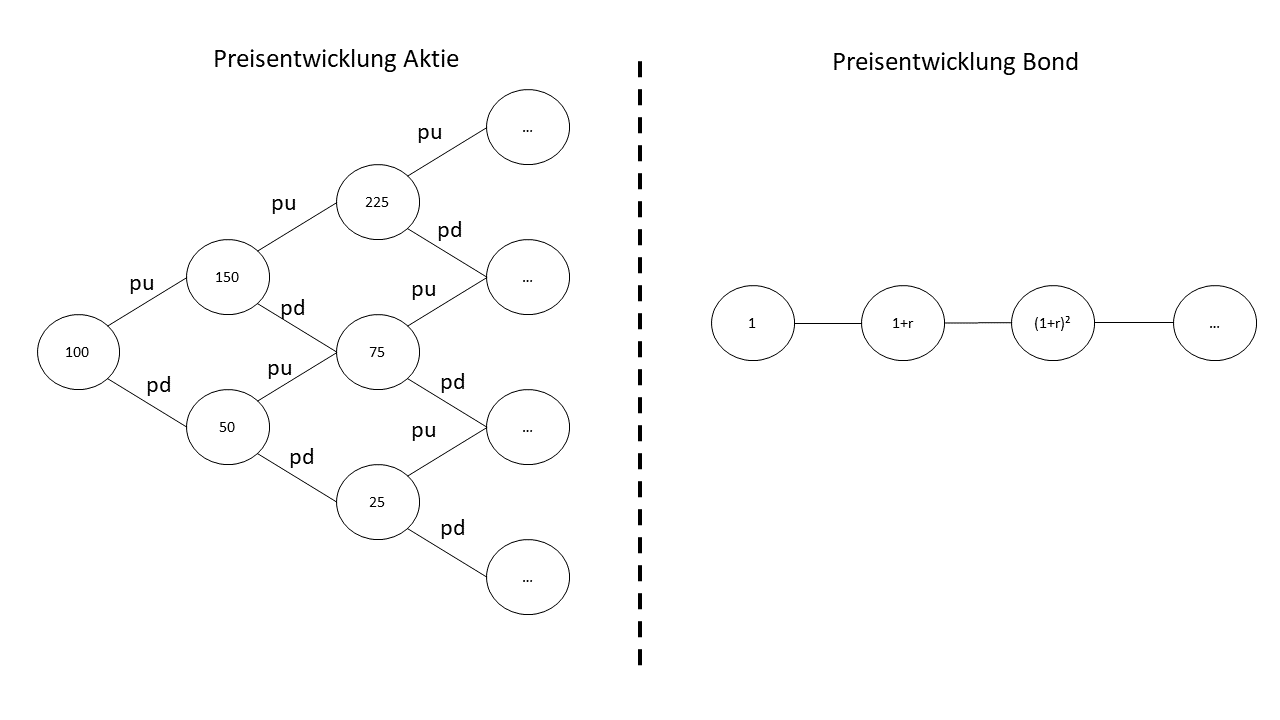
Fazit

Eigentlich ist jetzt alles wichtige zum CRR-Modell gesagt worden. Wir haben die wesentlichen Annahmen und Parameter des Modells zusammengefasst. Die obige Abbildung zeigt nochmal wie bemerkenswert einfach dieses Modell im Grunde ist. Man könnte das Modell noch hinreichend präziser beschreiben. Hier wurde beispielsweise auf eine detaillierte Angabe des zugrundeliegenden Wahrscheinlichkeitsraumes verzichtet. Ebenso habe ich unverschämterweise Gebrauch von stochastischen Prozessen gemacht, ohne näher darauf einzugehen. Dem interessierten Leser empfehle ich an dieser Stelle in den Büchern STOCHASTIC FINANCE, AN INTRODUCTION IN DISCRETE TIME von Hans Föllmer und Alexander Schied oder Arbitrage Theory in Continuous Time von Tomas Björk nachzuschlagen. Das erstere behandelt das CRR-Modell dabei sehr detailliert.

Hier das wesentliche nochmal zusammengefasst: Das CRR-Modell

• nimmt an, dass es keine Handelsbeschränkungen, Steuern, Gebühren oder Dividenden gibt
• setzt voraus, dass nur zwei Wertpapiere gehandelt werden. Ein risikoloses (Bond) und ein risikobehaftetes (Aktie)
• hat einen konstanten risikolosen Zinssatz r
• ist ein endliches (diskretes) Modell
• fordert, dass für jede Periode (mit gleicher Wahrscheinlichkeit) gilt, dass die Rendite \( r_u \) oder \( r_d \) ist
• erlaubt den beliebig granularen Kauf/Verkauf von Wertpapieranteilen

Offensichtlich ist unser Modell an vielen Stellen höchst angreifbar. So gibt es doch selbstverständlich Handelsbeschränkungen. Auch der Zinssatz für risikolose Wertpapiere unterliegt einer Wertänderung und so weiter. Es hängt ein wenig von den Ansprüchen des Modell-Nutzers ab. Wie präzise soll das Modell sein? Für was verwende ich das Modell? Welche Konsequenzen können meine Handlungen haben, die ich aus dem Modell ableite? Nutze ich das Modell für praktische Anwendungen oder sozusagen als Lehrmaterial? Modelle sind eigentlich nur Abbilder der Wirklichkeit, und können nie den Anspruch haben jedes Phänomen fehlerfrei zu beschreiben. Das weiß jeder Physiker, Architekt, Softwareentwickler, Handwerker, Mathematiker, Philosoph und sonst jeder, der sich mit Modellen der "Wirklichkeit" beschäftigt.

Ausblick

Im nächsten Teil werden wir über Arbitragefreiheit und Pricing sprechen. Die meisten Ökonomen setzen in ihren Modellen Arbitragefreiheit voraus. Wir werden ein einfaches Kriterium kennenlernen, mit dessen Hilfe man die Arbitragefreiheit im Modell nachprüfen kann. Es wird sich zeigen, dass die Arbitragefreiheit etwas mit der Existenz von Martingalmaßen zu tun hat (sozusagen "faire" Glücksspiele). Dieser Begriff wird uns dabei helfen ein Werkzeug zu entwickeln, um Derivaten einen fairen (arbitragefreien) Preis zuzuordnen und um Hedging-Strategien zu berechnen.