Einführung
In Teil 1 haben wir das CRR-Modell mit all seinen Annahmen definiert, sozusagen die Bühne aufgebaut. Zunächst wollen wir Derivaten einen fairen (arbitragefreien) Preis zuordnen (man spricht auch von Pricing).
Vereinfacht gesagt ist ein Marktmodell arbitragefrei, wenn es für einen Investor keine Möglichkeit für risikolose Gewinne gibt. In der Ökonomie ist die Annahme, dass Märkte weitestgehend arbitragefrei sind, weit verbreitet. Doch was heißt das genau und welche Konsequenz hat das für den Preis von Wertpapieren (speziell Derivaten)? Kann man so einen fairen Preis berechnen und Lässt sich das CRR-Modell auf Arbitragefreiheit hin prüfen? Die Antwort lautet Ja!
Arbitragefreiheit im CRR-Modell
In der klassischen Finanzmathematik gibt es eine Definition für eine Arbitragegelegenheit, die ich der Vollständigkeit halber hier genannt haben möchte (im Kontext des CRR-Modells).
Eine Arbitragegelegenheit ist ein Portfolio mit \( \xi^0_0 + \xi^1_0 S^1_0 \leq 0 \) und die beiden Bedingungen \( \mathbb{P}[\xi^0_T + \xi^1_T S^1_T \geq 0] = 1 \) und \( \mathbb{P}[\xi^0_T + \xi^1_T S^1_T > 0] > 0 \) erfüllt.
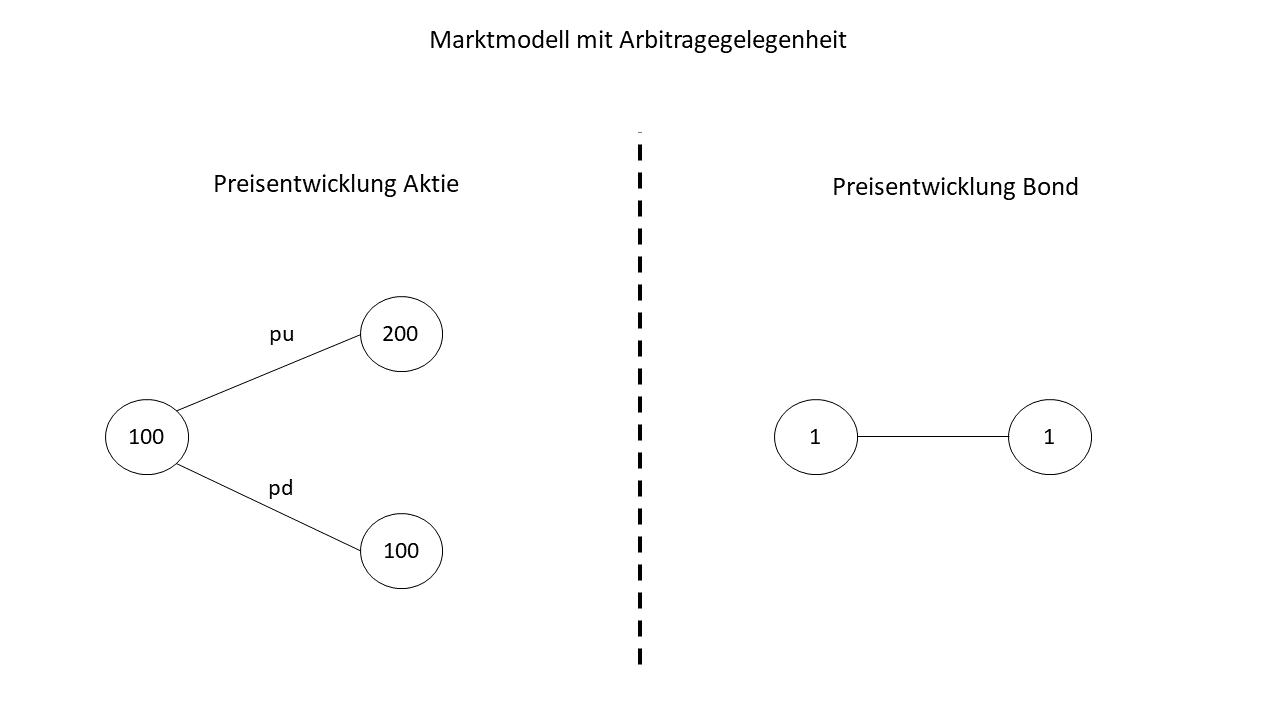
Es gibt mehrere Möglichkeiten diese Definition zu interpretieren. Ist beispielsweise die Aktie "zu billig" kann sich ein Investor zu einem gewissen Zinssatz Kapital bei einer Bank leihen. Das Kapital kann er in die Aktie stecken. D.h. der Investor benötigt kein eigenes Kapital. In jedem Fall wird der Investor keinen Verlust machen und es besteht sogar die Chance, dass er einen Gewinn macht. Der Leser mache sich weiterhin klar, dass es im mehrperiodischen Modell auch dann eine Arbitragegelegenheit gibt, wenn nur an einer Periode eine Arbitragegelegenheit existiert.
Der Begriff der Arbitragegelegenheit kann auch auf deutlich allgemeinere diskrete Finanzmarktmodelle ausgeweitete und theoretisch untersucht werden. Das soll bei einer anderen Gelegenheit getan werden. Die obige Definition wird in den folgenden Zeilen keine große Rolle spielen (das wäre anders, wenn man die folgenden Aussagen beweisen würde). Man ist aber gut beraten den oben dargelegten Sachverhalt im Hinterkopf zu behalten.
Wie kann man ein Finanzmarktmodell auf Arbitragefreiheit untersuchen? Wir gehen zunächst mal davon aus, dass \( p_u > 0 \) und \( p_d > 0 \) gilt. Man sollte sich an dieser Stelle vorstellen, dass jeder Investor unterschiedliche Wahrscheinlichkeitsparameter hat (vermutet). Das ist plausibel, da jeder Investor andere Erwartungen an die Zukunft hat. Der erste Fundamentalsatz der Wertpapierbewertung sagt aus, dass ein Markt genau dann Arbitragefrei ist, wenn es Wahrscheinlichkeitsparameter \( p^{*}_u > 0 \) und \( p^{*}_d > 0 \) gibt, welche der Martingaleigenschaft genügen, d.h. \( \mathbb{E}^{*}[X_{t+1} \mid \mathcal{F}_t] = X_t \) für alle \( t = 0, \cdots, T-1 \).
Der erste Fundamentalsatz ist im wörtlichen Sinne fundamental und ich empfehle sich bei Gelegenheit näher mit diesen Satz zu beschäftigen. Dem ein oder anderen könnte die obere Schreibweise für den sog. bedingten Erwartungswert Bauchschmerzen bereiten. Ich empfehle für solche grundlegenderen Themen das Buch Stochastik, Einführung in die Wahrscheinlichkeitstheorie und Statistik von Hans-Otto Georgii. Für den Anfang möge auch der entsprechende Wikipedia-Artikel genügen. Als Nachschlagewerk, um sich tiefer in finanzmathematische Themen einzulesen, empfehle ich nochmal das Buch STOCHASTIC FINANCE, AN INTRODUCTION IN DISCRETE TIME von Hans Föllmer und Alexander Schied.
Existieren nun solche Wahrscheinlichkeitsparameter, wie oben beschrieben? Die Antwort ist ja, genau dann, wenn \( r_d < r < r_u \). Man kann sie für das CRR-Modell sogar konkret ausrechnen. Es gilt
\[ X_t = \mathbb{E}^{*}[X_{t+1} \mid \mathcal{F}_t] \]
\[ = \frac{p^{*}_u \cdot (1 + u) \cdot X_t + p^{*}_d \cdot (1 + d) \cdot X_t}{1 + r} \].
D.h. es gilt der Term \( 1 + r = p^{*}_u \cdot (1 + u) + p^{*}_d \cdot (1 + d) \). Mit der Zusatzbedingung \( 1 = p^{*}_u + p^{*}_d \) erhält man ein lineares Gleichungssystem und erhält \( p^{*}_u = \frac{r - d}{u - d} \) und \( p^{*}_d = 1 - p^{*}_u = \frac{u - r}{u - d} \).
Es ist sogar so, dass das oben berechnete Wahrscheinlichkeitsmaß das einzige ist, welches die Martingaleigenschaft erfüllt. Man sagt, dass der Markt vollständig ist (diese Eigenschaft wird im Zusammenhang mit Hedging-Strategien wichtig werden).
Unter den obigen Bedingungen wissen wir nun außerdem, dass die Preise \( S_t = (1 + r)^{t} \cdot \mathbb{E}^{*}[X_{t+1} \mid \mathcal{F}_t] \) fair sein müssen (wir wissen jetzt schließlich, dass der Markt arbitragefrei ist). Dieses Prinzip lässt sich auch auf Derivate (europäische Contingent Claims) übertragen.
Europäische Contingent Claims
Ein europäischer Contingent Claim ist eine Zufallvariable (zufällige Größe) \( C_T \), welche die Bedingung \( 0 \leq C_T < \infty \) erfüllt. Dabei gibt es nur am Ende eine einzige Auszahlung (zum Zeitpunkt T). Ist \( C_T \) eine Funktion von \( S^1_0, S^1_1, \cdots, S^1_T \), so heißt \( C_T \) Derivat. Das Asset \( S^1 \) heißt dann Basiswert. Die Definition des Begriffs Derivat ist technisch nicht ganz korrekt. Eigentlich erfüllen Derivate eine bestimmte Messbarkeitseigenschaft (Begriff aus der Maßtheorie). Das soll aber an dieser Stelle nicht stören.
Wenn wir uns ein arbitragefreies CRR-Modell vorstellen, stellt sich sofort die Frage, ob die Arbitragefreiheit erhalten bleibt, wenn der Markt um ein weiteres Wertpapier erweitert wird. Im Fall von europäischen Contingent Claims lautet die Antwort Ja (nicht Trivial). Wir ernten nun die Früchte unserer Arbeit. Der Preis eines europäischen Contingent Claims zu einem Zeitpunkt ist damit
\[ \pi^C_t = \mathbb{E}^{*}[\frac{C_{T}}{(1+r)^{T-t}} \mid \mathcal{F}_t] \]
Ausblick
Es wurde jetzt viel Zeit mit der Formulierung des Modells und der Entwicklung der theoretischen Grundlagen aufgewendet (dabei kratzen wir eigentlich immer noch an der Oberfläche). Im nächsten Teil ernten wir die Früchte und berechnen den Preis für einige Derivate (europäische Contingent Claims). Analog werden wir anschließend über Hedging-Strategien sprechen, nachdem eine gewisse theoretische Grundlage aufgebaut wurde.
